Error Analysis of the Law of Total Tricks Length -4 -3 -2 -1 0 1 2 3 4 14 0.001 0.006 0.048 0.270 0.466 0.182 0.024 0.002 0.000 15 0.001 0.006 0.050 0.266 0.457 0.192 0.026 0.002 0.000 16 0.001 0.005 0.038 0.207 0.424 0.263 0.055 0.007 0.001 17 0.001 0.006 0.052 0.235 0.394 0.245 0.058 0.007 0.001 18 0.001 0.008 0.071 0.250 0.360 0.228 0.069 0.012 0.001 19 0.001 0.013 0.107 0.289 0.338 0.188 0.054 0.010 0.001 20 0.002 0.031 0.164 0.315 0.299 0.137 0.044 0.007 0.000 21 0.007 0.074 0.240 0.319 0.233 0.101 0.023 0.003 0.000 22 0.027 0.137 0.286 0.302 0.177 0.054 0.016 0.001 0.000 23 0.042 0.257 0.291 0.262 0.122 0.021 0.000 0.000 0.000 24 0.111 0.333 0.289 0.222 0.022 0.022 0.000 0.000 0.000 Totals 0.001 0.009 0.062 0.245 0.400 0.224 0.051 0.007 0.001
LoTT is a parabola not a straight line
#61

Posted 2014-November-07, 09:01
#62

Posted 2014-November-07, 12:01
Still need to think how to test this. A linear regression seems too much of a stretch here, given the data is highly non-normal.
#63

Posted 2014-November-07, 12:16
Most one way layout analysis of variance examples I've seen were testing if means of different groups are equal.
In this study the group means are known to be increasing as total trumps increase.
Also the group variances are not equal. Group variances increase as total trumps increase.
It is probably not that useful to know the exact equation for this parabola.
Total trumps is 21 or more only about 1.5% of the time. That is about 3 times every 8 sessions.
For trumps =14,,,18: tricks = trumps.
For trumps = 19 and 20: tricks are nearly equal to trumps.
For trumps > 20: tricks are clearly less than trumps.
That's probably all we need to know.
#64

Posted 2014-November-07, 12:29
In any case one thing is clear: the LOTT, in its E(tricks) formulation, breaks down for 20+ trumps, with a shift towards less tricks. Whether or not the shift is parabolic is another story, though in 1st order it should be so.
#65

Posted 2014-November-07, 18:03
#66

Posted 2014-November-07, 20:26
#67

Posted 2014-November-07, 22:47
Working points is more comprehensive than HCP. But too abstract for any of us to use without being allowed to view all 26 cards of our partnership.
The other independent variable is the joint suit pattern of both hands. This is best represented by combined trumps with a SST displacement adjustment.
E(tricks) = trumps + (HCP-20)/3 + SST
With a 4-4 trump fit and SST=4 the adjustment is + 1/6.
With a 5-4 trump fit and SST=4 the adjustment is - 1/3.
There is no fix adjustment for each SST value. It depends on the trump fit.
#68

Posted 2014-November-08, 05:50
 jogs, on 2014-November-07, 09:01, said:
jogs, on 2014-November-07, 09:01, said:
Thanks for posting the full tables. In that case, whatever the figure after the +/- in the summary table posted upthread are supposed to be, they are not the standard deviations (or the variances). The standard deviation for 24 total trumps, based on Ginsberg's frequencies, is 1.113 -- almost identical to the result of my sim (and the variance -- the square of the standard deviation -- is 1.240).
The actual standard deviations arising from Ginsberg's table are as follows.
14 15 16 17 18 19 20 21 22 23 24 0.898 0.912 0.986 1.034 1.118 1.145 1.188 1.216 1.240 1.148 1.113
#69

Posted 2014-November-08, 08:33
for i = 7,8,....,13 and for m = 0,1,....,6
SST is a table of displacement constants from the estimates based solely on trumps and HCP.
For any specific board the SST displacement is a discrete integer. In the general case it is a fractional amount.
xxx ------- x: There may be two additional tricks from ruffs
AKQ ------ x: No additional tricks.
------------------------
Every trump combination may produce a different set of SST.
6-2 fit is different from 4-4
SST=3+1 may be different from SST=2+2
E(tricks) = trumpsi+j + (HCP-20)/3 + SSTi+j,m+n
for i+j = 7,8,....,13 and i>=j
for m+n = 0,1...,6 where m is from the long trump hand and n may be from either hand.
There may be over 100,000 permutations. Luckily it is only necessary for us to know the directional bias of the displacement. That should put us ahead of the crowd.
#70

Posted 2014-November-08, 09:33
#71

Posted 2014-November-08, 10:40
#72

Posted 2014-November-08, 10:55
 jogs, on 2014-November-07, 18:03, said:
jogs, on 2014-November-07, 18:03, said:
Of course, it is important to be able to estimate our tricks. But it is also important to be able to estimate the total tricks.
These are two entirely different questions that are both important.
Estimating our tricks could e.g. tell us that we are have a 50% chance to make 3♠ and a 50% chance that it goes down. Does that tell us whether we should bid 3♠ over their 3♥? Not at all.
If we estimate 14 total tricks, meaning that they will take 5 or 6 tricks in 3♥, we should simply double 3♥. It will go down 3 or 4, which will be a lot better than making 3♠ or going down one.
If we estimate 20 total tricks, meaning that they will take 11 or 12 tricks in a heart contract, we should make them guess, and preferably make them guess wrong.
In these cases, it is fairly useless to know how many tricks we can take. It is more useful to know how many tricks the opponents can take.
I bought "I fought the Law" as soon as it came out. I was not amused when I read it. I expected an improved method for total tricks, better than the LoTT. That's what the title suggested and that is how Lawrence and Wirgren advertized it. Instead, I got yet-another-method-to-evaluate-hands-solely-for-offensive-purposes (after Milton Work count (4-3-2-1), Vienna count (7-5-3-1), zz points (3-2-1), LTC, Zar points, rule of 20, distribution points, fit points, shortness points, shortness points depending on fit, working points, ...). Frankly, I don't really care whether Lawrence/Wirgren works better than Zar points (or LTC or whatever). They promised me a book that would fight the Law, not Zar.
To me it felt like a book with the title "I fought McDonalds" where the author (perhaps even successfully, I don't care) argues why apple juice is tastier than orange juice (with somewhere a sentence "Burgers taste like $&%§% anyway"). But we all know that a book with the title "I fought orange juice" will not sell as well as "I fought McDonalds". (But perhaps "I fought OJ" would sell.
Rik
The most exciting phrase to hear in science, the one that heralds the new discoveries, is not “Eureka!” (I found it!), but “That’s funny…” – Isaac Asimov
The only reason God did not put "Thou shalt mind thine own business" in the Ten Commandments was that He thought that it was too obvious to need stating. - Kenberg
#73

Posted 2014-November-08, 13:33
 Trinidad, on 2014-November-08, 10:55, said:
Trinidad, on 2014-November-08, 10:55, said:
In uncontested auctions they aren't very helpful. In contested auctions we can't trust their bidding.
Normalize the boards where each side has 20 HCP, all in two suits.
S AKxxx S QJxx H xx H xx D AKx D QJxx C xxx C xxx
We can estimate our tricks at 9. Use the SST adjustment and lower the estimate to 8.
We know virtually nothing about their tricks.
S xxx
H AKxxx
D xx
C AKx
S x
H QJxx
D xxxx
C QJxx
They can make 10 tricks in hearts.
S xx
H AKxxx
D xxx
C AKx
S xx
H QJxx
D xxx
C QJxx
Now they can only make 8 tricks.
Our chances of estimating total tricks is much less reliable than estimating our own tricks.
#74

Posted 2014-November-08, 16:11
We guess looking at our shape that we probably don't have 9, meaning the actual total averages 17. We don't know if they have 8 or 10 so we take the average for calculation purposes; in the long run it'll balance out to about that. That's what the LoTT is for, the long run, not figuring out This Hand.
We have to estimate; it's the nature of the game. That's why cards have backs.
#75

Posted 2014-November-08, 16:58
 jogs, on 2014-November-08, 13:33, said:
jogs, on 2014-November-08, 13:33, said:
1) You don't give any decent arguments to support this statement. We just saw in this tread that a function describing the total number of tricks, only based on the number of trumps that both sides hold (no adjustments or anything), has a standard deviation of about 1 total trick. This scales to a standard deviation of 0.5 tricks for the number of tricks one side can take. I cannot think of a method that can predict the number of tricks with an accuracy of half a trick. Yet, you claim that estimating total tricks is much less reliable than estimating our own tricks. What magical method do you have that leads to a standard deviation of less than say 0.05 tricks? (I'll be nice to you and say that a factor of 10 is "much less".)
2) Suppose, for the sake or argument, that your statement would be true and estimating total tricks is indeed less reliable than estimating our own tricks, how does that mean that we should stop estimating total tricks when the situation clearly asks for a total trick estimate? If something is difficult, we should give up and throw our hands in the air? Remind me not to let you near my children.
Rik
The most exciting phrase to hear in science, the one that heralds the new discoveries, is not “Eureka!” (I found it!), but “That’s funny…” – Isaac Asimov
The only reason God did not put "Thou shalt mind thine own business" in the Ten Commandments was that He thought that it was too obvious to need stating. - Kenberg
#76

Posted 2014-November-08, 17:34
Clearly, even for E(tricks) the LOTT only holds approximately.
#77

Posted 2014-November-08, 19:21
 Trinidad, on 2014-November-08, 16:58, said:
Trinidad, on 2014-November-08, 16:58, said:
Rik
All those std dev calculations assume you actually know the total trumps. Which isn't true. Your trump estimates is often off by one and sometimes off by two or more.
Also std dev isn't linear. Variance is linear.
#78

Posted 2014-November-08, 19:48
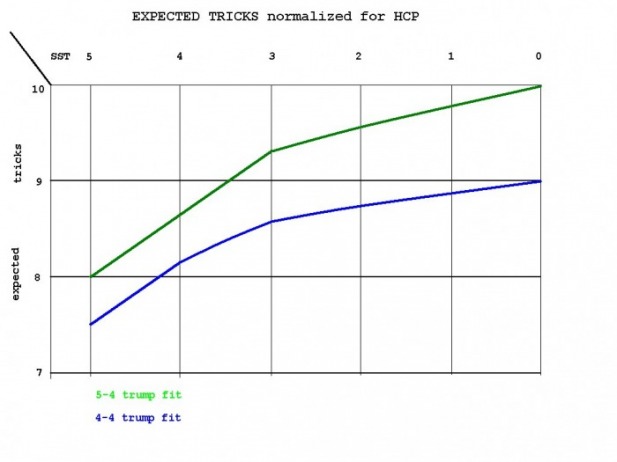
The green line is a 5-4 trump fit with observations taken from BBO minis. The HCP and tricks are shifted to HCP=20.
The blue line is a 4-4 trump fit with observations taken from a dataset of experts vs experts from the Richard Pavlicek site.
SST = short suit totals.
Our tricks
E(tricks) = trumps + (HCP-20)/3 + SST
We often know our combined trumps. We know our own contribution to SST. We only sometimes know the complete SST.
Well they also have their tricks.
E(tricks) = their trumps + (HCP-20)/3 + their SST
We have difficulty learning of their trumps. Nearly impossible to know their SST.
Anyone who thinks he knows total tricks of a board frequently is deluding himself.
#79

Posted 2014-November-09, 06:57
round[ E(tricks) ] = trumps
or
round[ E(tricks) ] = c + c1*trumps + c2*trumps^2
Edit: fixed formulae
#80

Posted 2014-November-09, 07:33
for total trumps <20: total tricks = total trumps
for total trumps >=20: total tricks = total trumps - (total trumps - 19)/2
In addition:
for total trumps <20: Use adjustments -as described in Cohen's books- but don't adjust by more than 1 total trick.
for total trumps >=20: Use your own judgement based on the location of controls/shortness and secondary fits to "adjust freely".
Rik
The most exciting phrase to hear in science, the one that heralds the new discoveries, is not “Eureka!” (I found it!), but “That’s funny…” – Isaac Asimov
The only reason God did not put "Thou shalt mind thine own business" in the Ten Commandments was that He thought that it was too obvious to need stating. - Kenberg

 Help
Help

